Trebuchet – The First Fling

We had our first test of the trebuchet with the full 600+ lbs of concrete, and well it a huge… Well just see for yourself!  This was the very first toss!

Photo sequence provided by Irotras! Thanks for the awesome shots!

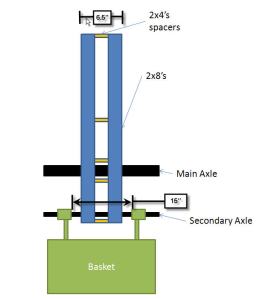
I don’t know how far it went exactly because we were so busy tossing the next pumpkin, but by my estimates the really heavy pumpkins (about 15+ lbs) were going about 100 ft. and the small pumpkins (about 6-8 lbs) were going about 200 ft.  That’s good, but it can be better!  One thing that was clearly evident in watching the trebuchet is that there is too much friction in the throwing arm and main axle joint.

I have some video that was taken with a real video camera, and once clean it up I will post that.

I would like to thank every one that helped me out on this project, specially my wife for being understanding and listening to the days and day of technobabel.

Trebuchet – Lockout/Safety

We wanted to add a safety on the trebuchet you don’t get an accidental misfire, since we are dealing with 600lbs dropping and generating 1 ton of force!!!!  This is a potentially deadly force.  Every care must be taken so as not to have a misfire.  That is why we designed a lockout mechanism or a safety mechanism.

It’s very simple it consists of a large diameter solid steel rod that is feed through the entire trebuchet.  This locks out the throwing arm.

Pushing the rod through enable people to get close to the trebuchet.  Then people can load the trebuchet with the ballistics, and put in the firing pin.

Trebuchet – Firing Pin Mechanism

I finished building the firing Pin Mechanism for the trebuchet.  It’s pretty simple.  There are three eyelet hooks; one on the throwing arm, and two attached to the frame.  I had to cut a slot into the trough so that the eyelets could be very close together. The photo below shows what it will look like underneath the trough.

I purchased a large 8″ nail that will act as the firing pin.  I’ll get a photo of that up here soon.

Trebuchet – Throwing Arm

So in explaining on how to size the primary axle, I realized something.  The same force that the primary axle experiences will also be experienced by the secondary axle!  This is bad, considering that I was planning on using something a lot smaller on the secondary axle.

However, this is not a complete disaster!  We had a couple of different options.

• Resize the axle
• make the axle strong (I don’t know how exactly)
• or distribute the forces closer to the edges

So that’s what we did!  Instead of having the two 2×8’s right next to each other we decided that we would put a 2×4 in between the board in order to space out the forces that the 2×8’s are putting on the secondary axle.

The forces are acting on the basket, throught the axle to the throwing arm.  The closer we bring the 2×8’s to the basket arms the less of a moment arm there is, which means less bending.  Just think for a minute.  We’ve all seen those large cat machines and all of those joints are made in a similar fashion to how we are making the basket joint.  If we look at the figure below the pin there is a tremenous amount of forces on that pin, but it completely in shear forces, and not bending.  It’s a lot easier to deal with shear forces, than it is to deal with bending forces.

Taken from http://www.cat.com/

So that what we did by separtating the beam and distributing the forces.

Other Resources

Trebuchet Design

Cement Blocks

Counterweight

Sizing the Axle (Part 1)

Sizing the Axle (Part 2)

A-Frames

Car Throwing Trebuchet

Cool Trebuchet Pictures

The bucket

Trebuchet – Cement Blocks

This weekend we had a strong surge and are very close to completing the Trebuchet!  A very special thanks to all of the those who helped!

In order to reach our goal of throwing a 6 lbs pumpkin the length of a football field we need to have a counterweight 100 times bigger.  So that means we need 600lbs of something.  Well, we looked around but couldn’t find anything that was dense enough, cheap enough.  Lead would be ideal, but where do we get 600 lbs of lead, and who wants to work with lead anyway?

So we went with the next best thing!  CEMENT!  According to the McGraw-Hill Encyclopedia of Science and Technology, “Volume generally assumed for the density of hardened concrete is 150 lb/ft^3 or 2400 kg/m^3.”

Since we need 600 lbs we need a volume of

600 lbs/150lbs/ft^3 = 4 ft^3

of cement.  This translates into 1.58 ft or approximately  20 inches on each side.   Our cement blocks are going to be 21.5 inches wide, and 19.5 deep, and 4 inches high.  We did this so the the cement blocks wouldn’t interfere with the throwing arm when the trebuchet arm is cocked back.   It will make sense once I get a picture up of that.  Anyway… here are the remain 3 blocks of concrete that are needed to make up the counterweight.

Other Resources

Trebuchet Design

Cement Blocks

Counterweight

Sizing the Axle (Part 1)

Sizing the Axle (Part 2)

A-Frames

Car Throwing Trebuchet

Cool Trebuchet Pictures

The bucket